复杂度

参考：
https://juejin.cn/post/6844903750985842695 。
https://github.com/biaochenxuying/blog/issues/29 。

什么是复杂度分析

复杂度分析是整个算法学习的精髓，使用数据结构与算法是为了能更快时间、更省空间地解决问题。因此，需要从 执行时间 和 占用空间 两个维度来评估数据结构与算法的性能。虽然我们能用代码准确的计算出执行时间，但是这也会有很多局限性。

• 数据规模的不同会直接影响到测试结果。比如同一个排序算法，排序顺序不一样，那么最后的计算效率的结果也会不一样，而如果恰好已经是排序好的了数组，那么执行时间就会更短。又比如如果数据规模比较小的话，测试结果可能也无法反应算法的性能。
• 测试的环境不同也会影响到测试结果。比如同一套代码分别在 i3 和 i7 处理器上进行测试，那么 i7 上的测试时间肯定会比 i3 上的短。

所以需要一个不用准确的测试结果来衡量，就可以粗略地估计代码执行时间的方法。这就是复杂度分析。

和性能测试相比，复杂度分析有不依赖执行环境、成本低、效率高、易操作、指导性强的特点。掌握复杂度分析，将能编写出性能更优的代码，有利于降低系统开发和维护成本。分别用时间复杂度和空间复杂度两个概念来描述性能问题，二者统称为复杂度。

大 O 复杂度表示法

估算下面代码的执行时间

function total(n) {
  let sum = 0;
  for (let i = 0; i < n; i++) {
    sum += i;
  }
}

我们假设每行代码执行的时间都一样记做 t，那么上面的函数中第 2 行需要 1 个 t 的时间，第 3 行 和 第 4 行分别需要 n 个 t 的时间，那么这段代码总的执行时间为 (2n+1)*t。

function total(n) {
  let sum = 0;
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      sum = sum + i + j;
    }
  }
}

同理，第 2 行需要一个 t 的时间，第 3 行需要 n 个 t 的时间，第 4 行和第 5 行分别需要 n² 个的时间，那么这段代码总的执行时间为 (2n²+n+1)*t 的时间。

从数学角度来看，我们可以得出个规律：代码的总执行时间 T(n) 与每行代码的执行次数成正比。

T(n) = O(f(n))

在这个公式中，T(n) 表示每行代码总的执行时间，n 表示数据规模的大小，f(n) 表示每行代码执行次数总和，O 表示代码的执行时间 T(n) 与 f(n) 表达式成正比。

所以上面两个函数的执行时间可以标记为 T(n) = O(2n+1) 以及 T(n) = O(2n²+n+1)。这就是大 O 时间复杂度表示法，它不代表代码真正的执行时间，而是表示代码随数据规模增长的变化趋势，简称时间复杂度。

由于时间复杂度描述的是算法执行时间与数据规模的增长变化趋势，所以 常量阶 、低阶 、系数 实际上对这种增长趋势不产生决定性影响，所以在做时间复杂度分析时 忽略 这些项。

而且当 n 很大时，我们可以忽略常数项，只保留一个最大量级。所以上面的代码执行时间可以简单标记为 T(n) = O(n) 和 T(n) = O(n²)。

时间复杂度分析

时间复杂度的全称是渐进时间复杂度，表示代码执行时间随数据规模增长的变化趋势。

算法的执行时间与每行代码的执行次数成正比，用 T(n) = O(f(n)) 表示，其中，T(n) 表示算法执行总时间，f(n) 表示每行代码执行总次数，而 n 往往表示数据的规模。

• 最好情况时间复杂度：在最理想的情况下，执行这段代码的时间复杂度。
• 最坏情况时间复杂度：在最糟糕的情况下，执行这段代码的时间复杂度。
• 平均情况时间复杂度：用代码在所有情况下执行的次数的加权平均值表示。
  （也叫加权平均时间复杂度或期望时间复杂度。）

只关注循环执行次数最多的一段代码

function total(n) {
  let sum = 0;
  for (let i = 0; i < n; i++) {
    sum += i;
  }
}

只有第 3 行和第 4 行执行次数最多，分别执行了 n 次，那么忽略常数项，此段代码的时间复杂度就是 O(n)。

加法法则：总复杂度等于量级最大的那段代码的复杂度

function total(n) {
  // 第一个 for 循环
  let sum1 = 0;
  for (let i = 0; i < n; i++) {
    for (let j = 0; j < n; j++) {
      sum1 = sum1 + i + j;
    }
  }
  // 第二个 for 循环
  let sum2 = 0;
  for (let i = 0; i < 1000; i++) {
    sum2 = sum2 + i;
  }
  // 第三个 for 循环
  let sum3 = 0;
  for (let i = 0; i < n; i++) {
    sum3 = sum3 + i;
  }
}

第一段 for 循环的时间复杂度为 O(n²)。
第二段 for 循环执行了 1000 次，是个常数量级，尽管对代码的执行时间会有影响，但是当 n 无限大的时候，就可以忽略。因为它本身对增长趋势没有影响，所以这段代码的时间复杂度可以忽略。
第三段 for 循环的时间复杂度为 O(n)。
总上，取最大量级，所以整段代码的时间复杂度为 O(n²)。

乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

function f(i) {
  let sum = 0;
  for (let j = 0; j < i; j++) {
    sum += j;
  }
  return sum;
}
function total(n) {
  let res = 0;
  for (let i = 0; i < n; i++) {
    res = res + f(i); // 调用 f 函数
  }
}

单独看 total 函数的时间复杂度就是为 T1(n)=O(n)，但是考虑到 f 函数的时间复杂度 T2(n)=O(n)。 所以整段代码的时间复杂度为 T(n) = T1(n) * T2(n) = O(n*n)=O(n²)。

多规模加法：多个参数控制多个循环相加的次数，取二者复杂度相加

function total(m, n) {
  let sum_1 = 0;
  for (let i = 0; i < m; i++) {
    sum_1 = sum_1 + i;
  }
  let sum_2 = 0;
  for (let j = 0; j < n; j++) {
    sum_2 = sum_2 + j;
  }
  return sum_1 + sum_2;
}

因为我们无法评估 m 和 n 谁的量级比较大，所以就不能忽略掉其中一个，这个函数的复杂度是有两个数据的量级来决定的，所以此函数的时间复杂度为 O(m+n)。

多规模乘法：多个参数控制多个循环嵌套的次数，取二者复杂度相乘

function total(m, n) {
  let sum = 0;
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      sum = sum + i * j;
    }
  }
}

同理，此函数的时间复杂度为 O(m*n)。

常见时间复杂度

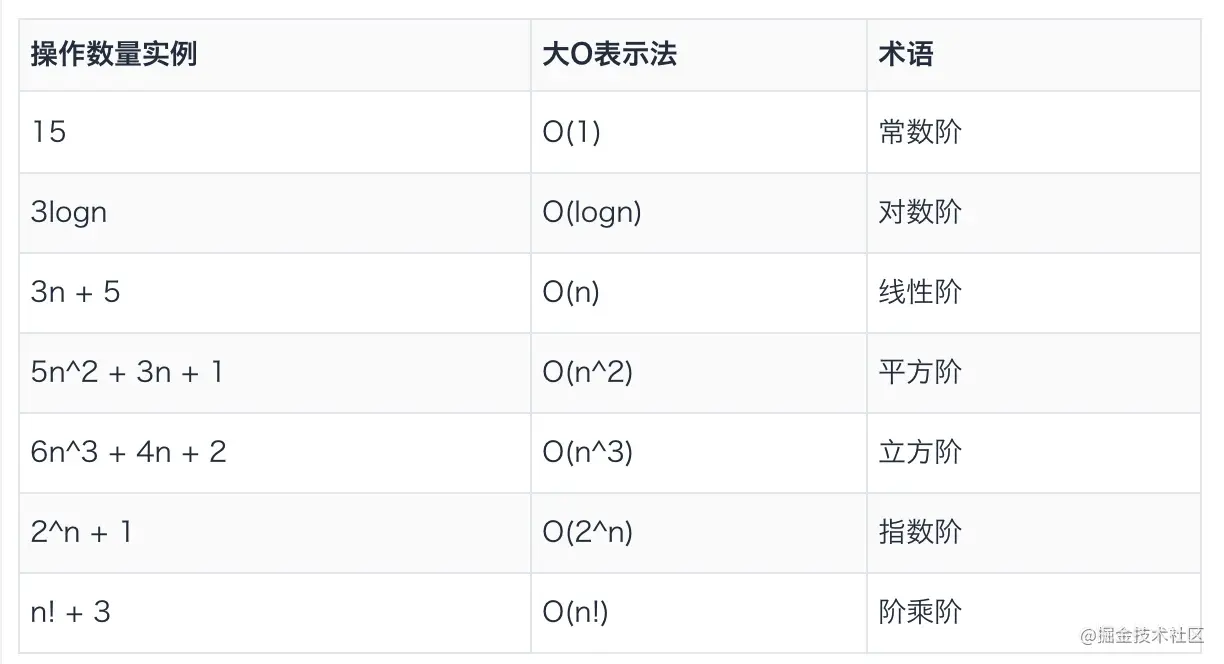
上图可以粗略的分为两类：多项式量级 和 非多项式量级 。

多项式量级会随着数据规模的增长，执行时间和空间占用按照多项式的比例增长。包括 O(1)（常数阶）、O(logn)（对数阶）、O(n)（线性阶）、O(nlogn)（线性对数阶）、O(n2) （平方阶）、O(n3)（立方阶）。

非多项式量级有 O(2ⁿ)（指数阶）和 O(n!)（阶乘阶）。随着数据规模的增长，非多项式量级的执行时间就会急剧增加，所以，非多项式量级的代码算法是非常低效的算法。

常用的时间复杂度所耗费的时间从小到大（效率从高到低）：
O(1) < O(logn) < O(n) < O(nlogn) < O(n²) < O(n³) < O(2ⁿ) < O(n!) < O(nⁿ)

O(1)

function total() {
  let sum = 0;
  for (let i = 0; i < 100; i++) {
    sum += i;
  }
}

虽然有这么多行，即使 for 循环执行了 100 次，但是代码的执行时间不随 n 的增大而增长，所以这样的代码复杂度就为 O(1)。

O(logn)

function total1(n) {
  let sum = 0;
  let i = 1;
  while (i <= n) {
    sum += i;
    i = i * 2;
  }
}
function total2(n) {
  let sum = 0;
  for (let i = 1; i <= n; i = i * 2) {
    sum += i;
  }
}

上面两个函数都有一个相同点，变量 i 从 1 开始取值，每循环一次乘以 2，当大于 n 时，循环结束。实际上，i 的取值就是一个等比数列。所以只要知道 x 的值，就可以知道这两个函数的执行次数了。那由 2^x = n 可以得出 x = log₂n，所以这两个函数的时间复杂度为 O(log₂n)。

实际上不管是以 2 为底、以 3 为底，还是以 10 为底，我们可以把所有对数阶的时间复杂度都记为 O(logn)。因为对数之间是可以互相转换的，log₃n = log₃2 _ log₂n，所以 O(log₃n) = O(C _ log₂n)，其中 C = log₃2 是一个常量，可以忽略。

那 O(nlogn) 的含义就很明确了，时间复杂度为 O(logn) 的代码执行了 n 次。

空间复杂度分析

空间复杂度的全称是渐进空间复杂度，表示代码存储空间随数据规模增长的变化趋势。

算法的空间复杂度通过计算算法所需的存储空间实现，算法的空间复杂度的计算公式记作：S(n) = O(f(n))，其中，n 为问题的规模，f(n) 为语句关于 n 所占存储空间的函数。

function initArr(n) {
  const arr = [];
  for (let i = 0; i < n; i++) {
    arr[i] = i;
  }
}

空间复杂度和时间复杂度类似，忽略掉常数量级，每次数组赋值都会申请一个空间存储变量，所以此函数的空间复杂度为 O(n)。

常见的空间复杂度有 O(1)、O(n)、O(n²)， 其他的话很少会用到。