排序

参考：
https://github.com/biaochenxuying/blog/issues/42 。
https://juejin.cn/post/6956624975600025613 。

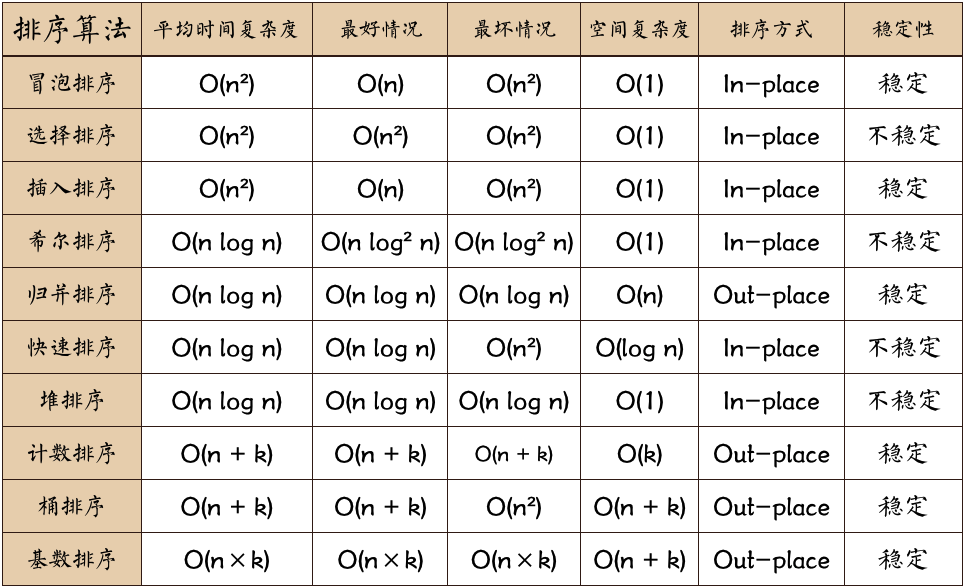
排序有冒泡排序、插入排序、选择排序、归并排序等十种经典方法。

分析一个排序算法，要从执行效率、内存消耗、稳定性三方面入手。

冒泡排序

思路

• 每次冒泡操作是对相邻的两个元素进行比较，看是否满足特定关系要求，若（不）满足就让它俩互换。
• 一次冒泡会让至少一个元素移动到它应该在的位置，重复 n - 1 次，就能完成 n 个数据的排序工作。

特点

• 优点：排序算法的基础，简单实用易于理解。
• 缺点：比较次数多，效率较低。
• 使用多个循环。

实现

普通：

function bubbleSort(arr) {
  const len = arr.length;
  for (let i = 0; i < len - 1; i++) {
    for (let j = 0; j < len - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        const temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }
  }
  return arr;
}

改进：

function bubbleSort2(arr) {
  const len = arr.length;

  for (let i = 0; i < len - 1; i++) {
    let hasChange = false;
    for (let j = 0; j < len - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        const temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
        hasChange = true;
      }
    }
    if (!hasChange) break;
  }
  return arr;
}

选择排序

思路

• 构建有序序列和未排序序列。认为第一个元素已经被排序，其余均为未排序序列的元素。
• 选择排序每次会从未排序序列中找到最小（大）的元素，将其放到已排序区间的开头（末尾）。

特点

• 使用多个循环。

实现

function selectSort(arr) {
  const len = arr.length;
  for (let i = 0; i < len - 1; i++) {
    let minIndex = i,
      temp = arr[i];
    for (let j = i + 1; j < len; j++) if (arr[j] < arr[minIndex]) minIndex = j;
    arr[i] = arr[minIndex];
    arr[minIndex] = temp;
  }
  return arr;
}

插入排序

插入排序又为分为 直接插入排序 和优化后的 拆半插入排序 与 希尔排序 。

思路

• 构建有序序列和未排序序列。认为第一个元素已经被排序，其余均为未排序序列的元素。
• 插入排序每次从未排序序列中取出一个元素，在有序序列中从后向前扫描，如果有序序列中的元素大于取出的元素，将该元素移到该元素的下一位置，直到找到相应位置并插入。

特点

• 使用多个循环。

实现

普通：

function insertSort(arr) {
  const len = arr.length;
  for (let i = 1; i < len; i++) {
    let preIndex = i - 1,
      current = arr[i];
    while (preIndex >= 0 && arr[preIndex] > current) {
      arr[preIndex + 1] = arr[preIndex];
      preIndex--;
    }
    if (preIndex !== i - 1) arr[preIndex + 1] = current;
  }
  return arr;
}

改进：

function binaryInsertionSort(arr) {
  const len = arr.length;
  for (let i = 1; i < len; i++) {
    let low = 0,
      high = i - 1,
      current = arr[i];
    while (low <= high) {
      let m = (low + high) >> 1;
      if (arr[i] >= arr[m]) low = m + 1;
      else high = m - 1;
    }
    for (let j = i; j > low; j--) arr[j] = arr[j - 1];
    arr[low] = current;
  }
  return arr;
}

归并排序

思想

归并排序采用的是分治思想。就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。

排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

特点

• 使用递归。

实现

function mergeSort(arr) {
  const len = arr.length;
  if (len < 2) return arr;
  let middle = Math.floor(len / 2),
    left = arr.slice(0, middle),
    right = arr.slice(middle);
  return merge(arguments.callee(left), arguments.callee(right));
}
function merge(left, right) {
  const result = [];
  while (left.length && right.length) {
    if (left[0] <= right[0]) result.push(left.shift());
    else result.push(right.shift());
  }
  while (left.length) result.push(left.shift());
  while (right.length) result.push(right.shift());
  return result;
}

快速排序

思想

先找到一个基准点（一般指数组的中部），然后数组被该基准点分割为两部分，依次与该基准点数据比较。如果比它小，放左边；反之放右边。左右分别用一个空数组去存储比较后的数据。最后递归执行上述操作，直到数组长度小于等于 1。

特点

• 优点：快速，常用。这是处理大数据最快的排序算法之一。
• 缺点：需要另外声明两个数组，浪费了内存空间资源。
• 使用递归。

实现

function quickSort(arr) {
  const len = arr.length;
  if (len <= 1) return arr;
  const midIndex = Math.floor(len / 2),
    valArr = arr.splice(midIndex, 1),
    midIndexVal = valArr[0],
    left = [],
    right = [];
  // 此时 len != arr.length
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] < midIndexVal) left.push(arr[i]);
    else right.push(arr[i]);
  }
  return arguments.callee(left).concat(midIndexVal, arguments.callee(right));
}

希尔排序

思想

先将整个待排序的记录序列分割成为若干子序列，分别进行直接插入排序。待整个序列中记录基本有序时，再对全体记录进行依次直接插入排序。

特点

• 使用多个循环。

实现

function shellSort(arr) {
  const len = arr.length;
  let gap = 1;
  while (gap < len / 3) gap = gap * 3 + 1;
  while (gap > 0) {
    for (let i = gap; i < len; i++) {
      const temp = arr[i];
      let j = i - gap;
      for (; j >= 0 && arr[j] > temp; j -= gap) arr[j + gap] = arr[j];
      arr[j + gap] = temp;
    }
    gap = Math.floor(gap / 3);
  }
  return arr;
}

堆排序

桶排序

计数排序

基数排序